| . | . | . | . | David McCracken |
Algorithmsupdated:2018.05.11 |
Many programmers try to meet each requirement as quickly as possible by matching it to an existing pattern, which in many cases is an actual piece of code. This seems simple initially but tends to produce cut-and-paste redundancy, making the program difficult to maintain. My approach is more analytical. The two analytical techniques I use most often are object-oriented and computational.
The ideal computational solution is algorithmic. For a circumscribed problem with well-studied solutions, such as sorting and compiler design, I analyze the problem to find the most appropriate existing solution. For problems with known general solutions but no existing good program model, I look for patterns that can be expressed in algorithmic rules. This is how I replaced a 2000-statement, 16-level deep sequence of nested functions used for blood cell typing with an algorithm comprising one small statement and a table. See Abbott CD3200-Algorithm Transformation.
Problems without known solutions require analysis. Unless a programmer is routinely analytical, they don't know how to approach these. Success often depends on patterns that are not specific to any one discipline. For example, a functionally equivalent algorithm is cheaper and more robust than precision. My satellite dish positioning algorithm (Satellite TVRO Patent) cost nothing in production yet performed better than precision solutions costing thousands of dollars. The same general pattern informs a solution to a flow cytometer problem at Abbott. The instruments required frequent recalibration to maintain precision that I discovered to be needed only because of fixed thresholds used to identify certain cell types. Replacing these with a pattern recognition algorithm not only reduced recalibration frequency but also increased accuracy on problematic samples. The touch pointer that I developed at IDT depends on sub-perceptive gesture algorithms developed using big data analysis methods similar to those used at Abbott to identify cell populations.
-30,46,531@0 -42,48,534@1 -32,44,542@2 -47,36,548@3 -33,37,552@4 -39,13,559@5 -27,13,562@6 -26,-4,568@7 -18,-19,566@8 -10,-24,566@9 -11,-46,560@10 10,-46,555@11 -3,-59,549@12 18,-59,543@13 1,-53,538@14 12,-53,535@15 12,-32,530@16 ------- Flick (17 points) ------- -27,43,529@0 -41,46,533@1 -54,46,538@2 -42,46,541@3 -55,43,544@4 -43,42,547@5 -49,21,554@6 -41,25,557@7 -50,5,564@8 -44,-8,568@9 -40,-22,566@10 -42,-42,562@11 -34,-47,561@12 -41,-60,556@13 -24,-60,552@14 -33,-63,550@15 -19,-63,546@16 -28,-61,543@17 -28,-47,534@18 -27,-36,531@19 ------- Flick (20 points) -------
Big data problems are usually solved by discovering patterns in a large data set, developing a matching rule, and then developing an algorithm to express the rule. Turing's halting problem teaches that only a human can discover useful patterns but few of us can discover a pattern in a sea of numbers. Consequently, an important step is presenting data in meaningful ways without presuming a pattern. Occasionally this happens without planning. For example, not until a user told me did I realize that the very high plotting speed of my cytometer data program could transform time into a non-occluding third dimension. More often, discovering the means of discovery is a deliberate process.
The first flick data that I encountered came from the three-by-three discrete button predecessor to my differential capacitance pointing device. No flick produced more than five points and half of the patterns indicated motion in the opposite direction. I had already formulated a plan for making this device usable for continuous touch but nothing could be done with this flick data. Although it might seem that just having more random data was not a solution, a fundamental analytics principle is that viewing data through a low-resolution aperture can hide subtle but important patterns. Whether that would prove true in this case could not be predicted but we would never know with the existing hardware. I developed the differential capacitive device to find out. Fortunately, by eliminating electrical noise and background capacitance, it is better than its predecessor in all ways.
My new device has a resolution of at least 1000 in each dimension compared to three in the old device. However, the flick data still looked random. This is not surprising. On such a small device, flicks often don't even contain one solid touch point. This is data that everyone else discards. To discover patterns that were not immediately obvious required presenting flick data in a comprehensible form. I decided to use my demo program for all pattern discovery not only to save time but also to have the mechanisms available for fine-tuning performance in a variety of customer applications.
At the most basic level, a flick is recorded as a sequence of points, characterized by X, Y, and weight values. Weight is a relative measure of Z determined by capacitive effect. To achieve the highest sample rate and consistent timing, I programmed my device firmware to capture the data in hard real-time. Consequently, although the development program is a Windows application and communicates with the device via USB, the points in a flick record are sampled at a precise rate.
Any one flick is of little value. We could find infinite irrelevant patterns in it. Many samples from different people in different environments are needed to weed these out. I automated a collection process in my demo program but volunteers still had to follow instructions so I also programmed a filter to discard obviously flawed data. My flick library eventually contained thousands of samples similar to the fragment shown here.
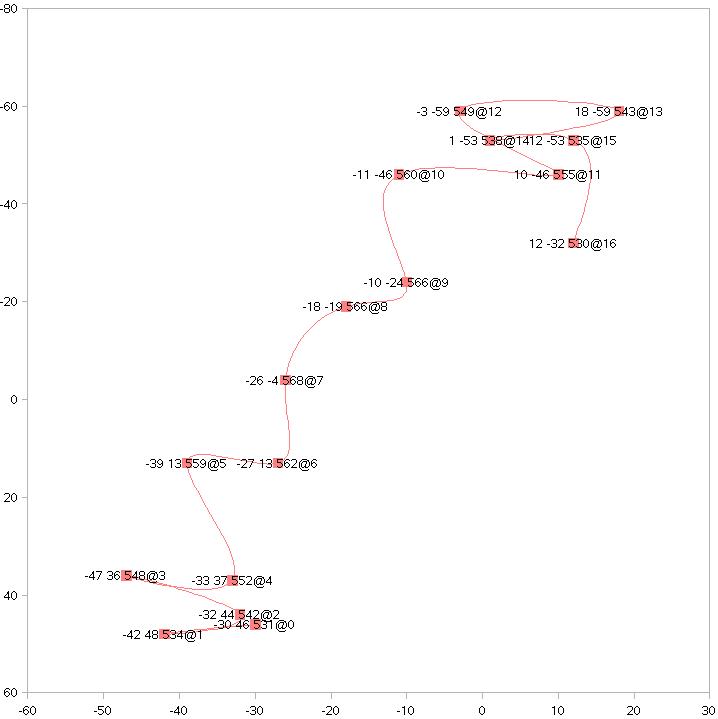
I found by experiment that showing each flick as a path with weighted points afforded the best view for seeing patterns. The actual paths are too random for any pattern to emerge from overlaid plots. I used Open Office (now Libre) Calc to create scatter plots like this north thumb flick example. For this plot I labeled each point with its X, Y, weight and sequence number. The first detected point is "-30 46 531@0", indicating -30 X value, 46 Y value, and weight of 531. Number 16 is the last point. The path from 0 to 3 suggests a westward flick but then the remainder show a definite eastward trend. That points 10 through 15 all lie above 16 suggests a southward rather than northward movement. This is actually one of the better thumb flicks, many of which reveal their true nature only in subtle patterns that dispute their more obvious features.
The absolute meaning of X and Y values is only relevant to determining the flick's length. The absolute value of weight is even less important. As I had discovered at Abbott, fixed references may impose counterproductive constraints. Obviously, environment and user differences create large absolute capacitance differences that overwhelm subtle patterns. Theoretically, these could be normalized by an average factor, but more importantly, many patterns emerge from point-to-point weight changes completely unrelated to absolute values. An important pattern is monotonic increase and decrease as the finger approaches and retreats ("touch" and "untouch"). Even the actual delta or delta rate (i.e. derivative of weight change) are relatively unimportant. Any non-monotonic deviation indicates user uncertainty, even though this is sub-perceptive.
------- Flick (17 points) ------- 0@0,E,5,Envelope 75% 173@170,W,8,Strong spread 75% 174@174,W,15,75% sequence split 249@176,W,18,75% strongest split 249@176,W,21,75% avg split 249@176,W,24,75% env split 291@173,W,14,50% sequence split 310@175,W,17,50% strongest split 310@175,W,20,50% avg split 315@172,W,13,25% sequence split 315@176,W,23,50% env split 328@174,W,16,25% strongest split 328@174,W,19,25% avg split 328@176,W,22,25% env split 345@170,W,9,All sequence split 349@175,W,12,All env split 353@173,W,10,All strongest split 353@173,W,11,All avg split 428@173,W,0,Real 441@169,W,3,Envelope 25% 441@169,W,4,Envelope 50% 441@172,W,6,Strong spread 25% 462@169,W,7,Strong spread 50% 572@155,NW,1,Envelope+real 572@155,NW,2,Envelope All
Many patterns emerged as meta-patterns, that is patterns of patterns. The flick "language" is significantly context-free, with grammatical patterns built on simpler patterns with constant syntax but varying semantic meaning. From this, I developed 25 different methods for interpreting a flick. The actual program code is surprisingly small and computationally cheap. I added a tuning mode wherein each method is applied to a flick and its answer recorded, as illustrated here. Like single-flick plots, this was initially useful to show that the methods were working as intended but determining which, if any, of these are best, requires statistical analysis on many samples. The coordination cost of doing this with post data collection tools was higher than the cost of adding the code to the demo program. In the statistic sampling mode, a user is instructed to repeatedly perform a certain flick specified by direction, length, and speed. Obviously bad examples are discarded but the remainder are considered a correct reference against which all of the methods are measured. At the end of each flick, all methods are invoked and their deviation from the reference recorded. At the end of each data set, the methods are ranked and the results logged.
fails, avg pos angle, cnt, avg neg angle, cnt,
avg angle err, worst angle error, method
0 85 86 0 0 12 47 0 Real
0 86 86 0 0 25 90 1 Envelope+real
0 76 86 0 0 25 90 2 Envelope All
0 76 86 0 0 27 90 3 Envelope 25%
0 68 86 0 0 35 90 4 Envelope 50%
0 46 84 -70 2 55 160 5 Envelope 75%
0 84 86 0 0 12 47 6 Strong spread 25%
0 82 86 0 0 13 47 7 Strong spread 50%
0 82 86 0 0 14 59 8 Strong spread 75%
0 82 86 0 0 11 51 9 All sequence split
0 82 86 0 0 11 51 10 All strongest split
0 82 86 0 0 10 41 11 All avg split
0 83 86 0 0 11 57 12 All env split
2 80 84 0 0 12 62 13 25% sequence split
3 80 83 0 0 13 53 14 50% sequence split
18 77 68 0 0 18 90 15 75% sequence split
2 81 84 0 0 14 90 16 25% strongest split
3 79 83 0 0 15 90 17 50% strongest split
18 72 68 0 0 23 90 18 75% strongest split
2 80 84 0 0 11 51 19 25% avg split
2 81 84 0 0 10 53 20 50% avg split
21 82 65 0 0 11 85 21 75% avg split
6 80 80 0 0 10 49 22 25% env split
8 81 78 0 0 10 49 23 50% env split
19 85 67 0 0 12 90 24 75% env split
I automated the tuning process as much as possible. The program leads a user through a sequence of flick types, automatically recording the statistical results. With the results from many users, it became apparent that even the best methods produce the correct answer only 80% of the time, are as likely as not to report the opposite direction when they are wrong, and have no measure of confidence to trigger a repeat request on questionable gestures.
I wrote an AWK program to calculate cumulative statistics from many data sets of each type of flick, that is many users doing one type, for example a fast northward thumb. A third level meta-pattern emerged from these results. The best methods are always right when they agree and they have different answers when they are wrong. Further, when the best disagree, other methods that are not very good alone are good at resolving the conflict. I developed a voting algorithm to take advantage of the pattern. A few best methods are always applied. When they don't agree, others are allowed to vote. Choosing the generally best methods is simple. Choosing the lesser ones and, equally important, the order of their application is determined by a second-order statistical analysis of how well they resolve particular types of conflicts.
Method 0 error=1700 uncomputables= 0 outliers= 0 Method 1 error=2300 uncomputables= 0 outliers= 0 Method 2 error=2600 uncomputables= 0 outliers= 0 Method 3 error=2600 uncomputables= 0 outliers= 0 Method 4 error=2400 uncomputables= 0 outliers= 0 Method 5 error=3607 uncomputables= 0 outliers= 4 Method 6 error=1700 uncomputables= 0 outliers= 0 Method 7 error=2500 uncomputables= 0 outliers= 0 Method 8 error=1952 uncomputables= 0 outliers= 1 Method 9 error=2300 uncomputables= 0 outliers= 0 Method 10 error=2233 uncomputables= 0 outliers= 1 Method 11 error=1760 uncomputables= 0 outliers= 1 Method 12 error=1700 uncomputables= 0 outliers= 0 Method 13 error=2600 uncomputables= 0 outliers= 0 Method 14 error=2666 uncomputables= 0 outliers= 1 Method 15 error=3995 uncomputables=10 outliers= 3 Method 16 error=2747 uncomputables= 0 outliers= 3 Method 17 error=2780 uncomputables= 0 outliers= 4 Method 18 error=2736 uncomputables= 1 outliers= 3 Method 19 error=1800 uncomputables= 0 outliers= 0 Method 20 error=2276 uncomputables= 0 outliers= 2 Method 21 error=1741 uncomputables= 5 outliers= 1 Method 22 error=1700 uncomputables= 0 outliers= 0 Method 23 error=1856 uncomputables= 0 outliers= 1 Method 24 error=1908 uncomputables= 2 outliers= 1
The result is near perfect flick interpretation with almost no sensitivity to user variation. However, there is some sensitivity to the physical design, particularly overlay (plastic) type and thickness and overall pad size. This was easily addressed by having the statistical method analyzer record the ideal method application schedule in a configuration file. After building a prototype or first article, an OEM can fine-tune the flick recognizer in less than 10 minutes.
[Conclusions] [Bubble Sort] [Selection Sort] [Insertion Sort] [Shell's Sort] [Merge Sort] [Heap Sort] [Quick Sort] [Quick Sort with Inline Swap] [No Swap Quick Sort] [Template Quick Sort]
/*********************************************************
File: sorts.cpp
Purpose: Demonstrates and tests various sorting functions,
including Bubble, Selection, Insertion, Shell, Merge, Heap, and Quick
using built in data sets, a list provided on the command line or a
generated list of random ints. Statistics, e.g. number of swaps, are
reported. One or all functions can be timed with repeated invocations
to produce meaningful times on small data sets. I developed this
under Linux but it is a console program using only the standard C
library. Only the LINES and COLUMNS environment variables, from
termcap, are Linux-specific and these could be defined in Windows.
......................... Notes ....................................
DISPLAY
What to display is automatically determined based on operation
selection. If the command line includes Rx then any other arguments
are ignored and only a list of x random numbers is displayed. If the
command line include Tx then, to avoid interfering with timing,
nothing is displayed other than the final timings. Note that Tx has
no effect on Fx, Dx, or user-defined data set arguments.
If the command line includes neither Rx nor Tx then the data set
before and after sorting is displayed for each invocation of a sort.
If the command line selects one function then the sorting statistics
are reported for each data set. Otherwise, the statistics are
reported after all sorting is done. The display is arranged by sort
function under each data set to make it easy to see function
differences. Additionally, the culmulative statics are displayed.
The show function is called just to display data sets. It and
indent are copied from quick.cpp, whose purpose is to display the
activity of quicksort in greater detail. show is directed by the
showWhat bitmap and its "local" argument. The SHOW_GLOBAL,
SHOW_LOCAL1, and SHOW_LOCAL flags are remnants of quick.cpp and are
not used here. That program also includes a flag to turn on display
of indices during sorting, producing a very detailed execution trace.
TIMING RESULTS
For small datasets sorting is so fast that it can't be accurately
measured if applied only once. To increase accuracy, the repetition
argument can be very high, making absolute times relatively
meaningless. A normalized result is also output where the slowest
sort is 100% and all others are relative to this. Heapify is included
here but not considered the best even though it is always the
fastest. Here the results are arranged from worst to best.
The following results were taken before drr (run-time) and no stat
recording (compile-time) options were implemented. Further testing
shows not only absolute but also relative timing sensitivity to both
of these. The best way to test these would be to run with dr (not
drr) repeatedly and average the times. It would also be good to
record an instance of drr for each list count before testing the
timing effects of algorithm changes.
These tests also don't include QuickNoSwap, which was implemented
later. Compared to standard quick (inline swap) its relative times
are 75% on 10, 55% on 100, 68% on 1000, 69% on 10000, 66% on 100000,
66% on 1000000. i.e. it averages 33% faster.
./sorts dr10 t1000000
Merge time = 100% (worst)
Shell time = 64%
Bubble time = 55%
Heap time = 55%
Insertion time = 46%
Quick time = 46%
Selection time = 38% (best)
Heapify time = 20%
./sorts dr100 t10000
Bubble time = 100%
Selection time = 67%
Insertion time = 43%
Merge time = 33%
Heap time = 30%
Shell time = 29%
Quick time = 23%
Heapify time = 3%
./sorts f-bs dr1000 t1000
Insertion time = 100%
Shell time = 19%
Merge time = 10%
Heap time = 10%
Quick time = 8%
Heapify time = 1%
./sorts f-bsi dr10000 t100
Shell time = 100%
Heap time = 12%
Merge time = 11%
Quick time = 9%
Heapify time = 1%
./sorts f-bsil dr100000 t50
Heap time = 100%
Merge time = 84%
Quick time = 71%
Heapify time = 8%
./sorts f-bsil dr1000000 t1
Heap time = 100%
Quick time = 68%
Merge time = 58%
Heapify time = 5%
At n = 10, selection is best and merge is worst.
1.2 times faster than quick and insertion.
1.5 times faster than heap and bubble.
1.7 times faster than shell.
2.6 times faster than merge.
At n = 100, quick is best and bubble is worst.
1.3 times faster than shell and heap.
1.4 times faster than merge.
1.9 times faster than insertion.
2.9 times faster than selection.
4.3 times faster than bubble.
At n = 1000, quick is best and insertion is worst
(bubble and selection are excluded)
1.25 times faster than heap and merge.
2.4 times faster than shell.
12.5 times faster than insertion.
At n = 10,000 quick is best and shell is worst
(insertion is now also excluded).
1.2 times faster than merge and heap.
11 times faster than shell.
At n = 100,000 quick is best and heap is worst
(shell is now also excluded)
1.2 times faster than merge.
1.4 times faster than heap.
At n = 1,000,000 merge is fastest and heap is worst.
1.2 times faster than quick.
1.7 times faster than heap.
quick uses stack for recursion and merge used both stack and heap
memory. However, merge uses the same amount of stack (logn) in all
cases as quick uses in the best case. In the worst case, quick uses
nearly n stack. None of the other sorts require auxiliary memory. The
depth stat is recorded only for quick and merge. It confirms theory:
n = 10 logn = 4 quick = 4 merge = 4
n = 100 logn = 7 quick = 10 merge = 7
n = 1000 logn = 10 quick = 23 merge = 10
n = 10000 logn = 14 quick = 30 merge = 14
n = 100000 logn = 17 quick = 40 merge = 17
n = 1000000 logn = 20 quick = 51 merge = 20
Compared to quick, heap is:
1.2 times slower at n = 10
1.3 times slower at n = 100
1.2 times slower at n = 1000
1.3 times slower at n = 10000
1.4 times slower at n = 100000
1.5 times slower at n = 1000000
i.e. heap ranges from 20% to 50% slower than quick.
Compared to merge, heap is:
1.8 times faster at n = 10
1.1 times faster at n = 100
equal at n = 1000 and n = 10000
1.2 times faster at n = 100000
1.7 times slower at n = 1000000
Conclusions
1. Don't use bubble or selection for anything. Selection is the
fastest at n = 10 but all functions execute quickly on this small set.
2. For n < 100 if recursion is ok then use quick. If recursion is not
ok then use insertion or heap.Insertion is faster for smaller n while
heap is faster for larger.
3. For n > 100 use quick unless no recursion, in which case use heap.
****************************************************************/
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <ctype.h>
#include <time.h>
//================= DATA AND DECLARATIONS ============================
// -------------------------------------------------------------------
// COMPILE-TIME OPTIONS
// ...................................................................
// Turn statistics recording on or off. Recording may reduce relative
// timing accuracy. e.g. merge vs. heap on dr1000000 is 43% without
// recording but 58% with recording.
#if 1
#define STAT(P,S,I) P[S] += I
#define STAT_COPIES(P,N,B) P[ COPIES ] += N, P[ COPYBYTES ] += B
#define STAT_DEPTH_INC incDepth()
#define STAT_DEPTH_DEC depth--
#else
#define STAT(P,S,I)
#define STAT_COPIES(P,N,B)
#define STAT_DEPTH_INC
#define STAT_DEPTH_DEC
#endif
// Make swap inline or not. Define as blank for not inline. This
// actually has little impact on performance but is provided as an
// option just to demonstrate and, in particular, to show that
// eliminating swapping altogether is much more significant than
// making it inline. The quicksort with embedded swapping is < 1%
// faster than with inline swap function (probably due to
// optimization) and it is 1.5% faster than with non-inline. In
// contrast, the noswap quicksort is 40% faster than quicksort with
// embedded swap.
#define INLINESWAP inline
#define DIM(A) (int)( sizeof(A) / sizeof( A[0] ))
#define BEYOND(A) ( A + DIM( A ))
//typedef unsigned int UINT;
enum
{
SHOW_NOTHING,
SHOW_GLOBAL = 1, // Show the current global list at
// each repeat/recurse.
SHOW_LOCAL1 = 2, // Show the local list at the beginning
// of the function.
SHOW_LOCAL = 4, // Show the local list after each change.
SHOW_EACH_DAT_STAT = 8, // Show stats after each sort (of one list)
SHOW_BASIC = 16, // Show function name heading and global
// list before and after.
};
int showWhat = SHOW_BASIC;
int dat0[] = { 2, 9, 4, 3, 1, 8, 7};
int dat1[] = { 7, 0, 4, 9, 8, 2, 1, 6, 3};
int dat2[] = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
int dat3[] = { 9, 8, 7, 6, 5, 4, 3, 2, 1, 0};
int dat4[] = { 3,6,7,5,15,12,9,1,2,10,16,0,11,8,43,29,18,13,22,21,4,
14,23,20,46,27,17, 25,50,38,34,36,19,39,87,26,59,37,35,47,33,28,30,49,
51,41,24,32,54,58,56,88,80,40,64,48, 45,66,92,71,79,70,42,52,67,55,31,
62,72,98,94,65,74,84,108,110,53,121,44,68,129,77,89,57, 106,96,60,86,
93,99,73,119,63,111,81,82,61,83,75,102}; // 100
static struct
{
int *list ; int cnt ;
} datLists[] = {
{ dat0, DIM( dat0 )},
{ dat1, DIM( dat1 )},
{ dat2, DIM( dat2 )},
{ dat3, DIM( dat3 )},
{ dat4, DIM( dat4 )},
};
enum
{
DSEL_USER = -1, DSEL_ALL = DIM( datLists )
}; // pseudo-values for data
// select. 0-DIM(datLists) - 1 selects one of the built-ins.
// >= DSEL_ALL selects all.
typedef void (SORTFUNC)( int *list, int cnt );
SORTFUNC bubbleSort, selectionSort, insertionSort, shellSort,
mergeSort, heapSort, quickSort, quickSortEs, quickSortNs, heapify;
// In the funcs table, if a function's select member is false, that
// function will be invoked only if explicitly requested by fx. f-x
// and no f argument at all select only those functions whose select
// is true. Non-selected functions are: - heapify only transforms the
// input to a heap, which is partially sorted and may have some value
// on its own. This function is very fast so if it can be of any use,
// it should be used. - quickSortEs (QuickEmbedSwap) exists to show
// that embedded swap affords essentially the same performance as
// inline swap, which is only marginally better than non-inline.
static struct
{
SORTFUNC *func; char *name; char cid; bool select; clock_t ticks;
} funcs[] = {
{ bubbleSort, (char*)"Bubble", 'B', true, 0},
{ selectionSort, (char *)"Selection", 'S', true, 0},
{ insertionSort, (char *)"Insertion", 'I', true, 0},
{ shellSort, (char*)"Shell", 'L', true, 0},
{ mergeSort, (char *)"Merge", 'M', true, 0},
{ heapSort, (char *)"Heap", 'H', true, 0},
{ quickSort, (char*)"Quick", 'Q', true, 0},
{ quickSortEs, (char*)"QuickEmbedSwap", 'E', false, 0},
{ quickSortNs, (char*)"QuickNoSwap", 'N', true, 0},
{ heapify, (char *)"Heapify", 'P', false, 0},
};
int nameFieldLen = DIM( "QuickEmbedSwap:" );
// Length of longest sort type name.
enum
{
CALLS, DEPTH, COMPARES, SWAPS, COPIES, COPYBYTES, DIM_STATS
};
char* statNames[] = {
(char*)"calls",
(char*)"depth",
(char*)"compares",
(char*)"swaps",
(char*)"copies",
(char*)"copy_bytes",
};
int stats[ DIM( funcs ) ][ DIM( datLists ) ][ DIM_STATS ];
int *statPtr; // e.g. stats[ fsel ][ dsel ].
int recursion; // Current recursion level.
int* testDat = 0;
#define MAX_USER_INPUT_DAT 100
int* userDat = 0;
size_t userDatCnt = 0;
clock_t maxTick;
int slowest;
int depth;
int maxDepth;
bool randomRepeat = false; // If DR then randomRepeat = false
// and synthesized random data is different at each invocation. If
// DRR then randomRepeat = true and synthesized data is the same
// every time.
//============================== FUNCTIONS =======================
// ------------------------------ indent -------------------------
// Print two spaces for each level of recursion to indent subsequent
// print output.
// ...............................................................
void indent( void )
{
for( int indent = 1 ; indent < recursion ; indent++ )
printf( " " );
}
// -------------------------------- show ----------------------------
// Print the given int list according to the global control setting
// showWhat and the given local identification. This may print
// nothing or the global list or the local sublist. It may or may not
// print the legend GLOBAL or LOCALx where x is the local ID, which
// tells at what point in the sort code we are showing the sublist.
// Returns: Nothing
// Arguments:
//- int *list points to the int list.
//- int cnt is the number of elements in the list.
//- int local tells the local point in the sort routine if greater
// than 0. 0 indicates that this is global. In either case, format is
// controlled by showWhat. If local is -1, the list is printed
// unconditionally and without any legend.
// Global:
//- showWhat bitmapped control word
//-- 0 (SHOW_NOTHING) This is the complete value, not a bit flag.
//-- 1 (SHOW_GLOBAL) Print the list if local is 0. If any other
// bit is also set, the GLOBAL legend is printed before the list.
//-- 2 (SHOW_LOCAL1) Print the list only if local is 1.
//-- 3 (SHOW_LOCAL) Print the list if local is 1 or greater.
//
// ...................... notes ..................................
// SHOW_NOTHING
// This exists because the callers don't test showWhat before
// calling. If we only want to show the initial unsorted list and
// final sorted version then SHOW_NOTHING blocks all print output
// from the sort function. The control function calls show with
// local = -1 to print the list.
// ...............................................................
void show( int *list, int cnt, int local, char *datLegend = 0 )
{
if( local >= 0 )
{
switch( showWhat )
{
case SHOW_NOTHING:
return;
case SHOW_GLOBAL: // Only SHOW_GLOBAL
if( local > 0 )
return; // This is a local
break; // Print list without legend.
default: // Some combination of SHOW_GLOBAL,
// SHOW_LOCAL1, SHOW_LOCAL
if( local == 0 ) // global
{
if( ( showWhat & SHOW_GLOBAL ) == 0 )
return;
printf( "GLOBAL " );
}
else if( showWhat & SHOW_LOCAL ||
( showWhat & SHOW_LOCAL1 && local == 1 ) )
{
indent();
printf( "Local%d: ", local );
}
else
return;
}
}
if( showWhat & SHOW_BASIC )
{
if( datLegend != 0 )
printf( datLegend );
for( int *end = list + cnt ; list < end ; list++ )
printf( "%d ", *list );
putchar( '\n' );
}
}
// -------------------------- incDepth --------------------------
void incDepth( void )
{
depth++;
if( depth > maxDepth )
maxDepth = depth;
}
// -------------------------------- swap ------------------------
INLINESWAP void swap( int *i1, int *i2 )
{
STAT( statPtr, SWAPS, 1 );
int temp = *i1;
*i1 = *i2;
*i2 = temp;
}
// ====================== SORT FUNCTIONS ===================
// --------------------- Bubble Sort ------------------------
void bubbleSort( int *list, int cnt )
{
int mainIdx;
int idx;
STAT( statPtr, CALLS, 1 );
for( mainIdx = cnt - 1 ; mainIdx > 0 ; mainIdx-- )
{
for( idx = 0 ; idx < mainIdx ; idx++ )
{
STAT( statPtr, COMPARES, 1 );
if( list[ idx ] > list[ idx + 1 ] )
swap( list + idx, list + idx + 1 );
}
}
}
// ------------------- Selection Sort ---------------------------
void selectionSort( int *list, int cnt )
{
int mainIdx;
int idx;
STAT( statPtr, CALLS, 1 );
for( mainIdx = cnt - 1 ; mainIdx > 0 ; mainIdx-- )
{
for( idx = 0 ; idx < mainIdx ; idx++ )
{
STAT( statPtr, COMPARES, 1 );
if( list[ idx ] > list[ mainIdx ] )
swap( list + idx, list + mainIdx );
}
}
}
// -------------------- Insertion Sort -----------------------
void insertionSort( int *list, int cnt )
{
STAT( statPtr, CALLS, 1 );
int lsi; // Last sorted index, i.e. index of right-most
// element of sorted sublist.
int idx;
int val;
for( lsi = 0 ; lsi < cnt - 1 ; lsi++ )
{
STAT( statPtr, COMPARES, 1 );
val = list[ idx = lsi + 1 ];
if( val > list[ lsi ] )
continue;
for( ; idx > 0 ; idx-- )
{
STAT( statPtr, COMPARES, 1 );
if( list[ idx - 1 ] > val )
{
STAT( statPtr, COPIES, 1 );
list[ idx ] = list[ idx - 1 ];
}
else
break;
}
STAT( statPtr, COPIES, 1 );
list[ idx ] = val;
}
STAT( statPtr, COPYBYTES, statPtr[ COPIES ]);
}
// -------------------- Shell's Sort -------------------------
// Selection ID = 'L'
void shellSort( int *list, int cnt )
{
int lsi; // Last sorted index, i.e. index of right-most
// element of sorted sublist.
int val;
int first;
int last;
int mid;
int move;
STAT( statPtr, CALLS, 1 );
for( lsi = 0 ; lsi < cnt - 1 ; lsi++ )
{
val = list[ lsi + 1 ];
STAT( statPtr, COMPARES, 1 );
if( val > list[ lsi ] )
continue;
first = 0;
if( lsi > 0 )
{
last = lsi;
while( 1 )
{
mid = ( last + first ) / 2;
STAT( statPtr, COMPARES, 1 );
if( list[ mid ] < val )
first = mid + 1;
else
last = mid - 1; // If mid is 0 last will be -1.
if( first >= last ) // It's ok if last is -1 because we will be
break; // using first, which will be 0.
}
}
STAT( statPtr, COMPARES, 1 );
if( list[ first ] < val )
++first;
move = 1 + lsi - first;
if( move == 1 )
list[ first + 1 ] = list[ first ];
else
memmove( list + first + 1, list + first, move * sizeof( int ));
list[ first ] = val;
STAT_COPIES( statPtr, 2, ( move + 1 ) * sizeof( int ));
}
}
// ========================= Merge Sort =========================
// Merge sort divides the list into two sublists and recurses on
// each. Upon return, the two lists are merged. It is not feasible
// for the sublists and merging to both be in-place because merging
// in-place would overwrite some elements of the sublists before they
// can be merged. The cheapest approach (but not parallelizable) is
// to do the sublists in-place and merge into a scratchpad allocated
// outside of the function. The merged block is copied back into the
// original. If not parallelized then only one iteration of the
// function at a time uses the scratchpad so only one copy is needed,
// but it must be as large as the full list for the top level merge.
int *mergeBuffer;
// -------------------------- mergeSorta ------------------------
// ........................... notes ............................
// RECURSION
// In the classic description, mergesort recurses until the list
// contains only one element. My version checks the length and stops
// before recursing on a sublist of only one element.
// ..............................................................
void mergeSorta( int *list, int cnt )
{
int lcnt;
int idx;
int lidx;
int ridx;
STAT( statPtr, CALLS, 1 );
STAT_DEPTH_INC;
lcnt = cnt / 2;
if( lcnt > 1 )
mergeSorta( list, lcnt );
if( cnt > 2 ) // At 3, left = 1 but right = 2.
mergeSorta( list + lcnt, cnt - lcnt );
for( lidx = 0, ridx = lcnt, idx = 0 ; idx < cnt ; idx++ )
{
STAT( statPtr, COMPARES, 1 );
mergeBuffer[ idx ] =
lidx >= lcnt ? list[ ridx++ ] :
ridx >= cnt ? list[ lidx++ ] :
list[ lidx ] <= list[ ridx ] ? list[ lidx++ ] :
list[ ridx++ ];
}
STAT_COPIES( statPtr, 1, cnt *= sizeof( int ));
memcpy( list, mergeBuffer, cnt );
STAT_DEPTH_DEC;
}
// ------------------- mergeSort -------------------------------
// Purpose: Front end for mergeSorta just to emphasize that merge
// sort needs a separate buffer, which is allocated and freed here.
// This contributes only marginally to execution time, e.g. 10% with
// small lists, where the effect would be greatest. I tested with
// both allocated and static. Static can't be used with the time test
// with command line declaration of random list size, which may be
// very large.
// ................................................................
void mergeSort( int *list, int cnt )
{
mergeBuffer = (int *)malloc( cnt * sizeof( int ));
mergeSorta( list, cnt );
free( mergeBuffer );
}
// ======================== HEAP SORT ===================
// The int list is treated as a max heap. list[0] is root and the
// parent of list[1] and list[2]; list[1] is the parent of list[3]
// and list[4]; list[2] is the parent of list[5] and list[6]; etc.
// The children of any idx are idx * 2 + 1 and idx * 2 + 2. The
// parent of any idx is ( idx - 1 ) / 2. Given an array, the first
// step of heapsort is to heapify it. This is done by heapifying each
// branch, starting at the parent of the last element and working
// backward to the beginning. Then the heap is transformed into a
// sorted list from smallest to largest by swapping the first (always
// max) element with the last, re-heapifying from the first, and
// repeating with the next-to-last, etc. down to the beginning. This
// sounds like a lot of resorting but heapifying the root branch
// takes only logn.
// The functions that comprise heapsort must always see the entire
// list because parent and child relationships are determined
// entirely by indices. If the heap were implemented with two-way
// pointers between parents and children then it would be possible to
// pass sublists similarly to recursive sorts like quick and merge.
#define parent(I) ((I-1)/2)
#define lchild(I) (I*2 + 1)
// --------------------- siftDown ----------------------------------
// Purpose: For the given branch of a binary heap, enforce the heap
// criteria that each parent be larger than both of its children.
// Arguments:
//- int *list is the beginning of an array organized as a heap.
//- int root is the index of the root of the branch to be heapified.
//- int last is the index of the last element of the entire list.
// Note that this is not count, as for the heapify and heapSort
// functions, only because last is used here. Instead of <= last
// and < last, we could use < cnt and < cnt - 1.
// ................................ notes .......................
// OPERATION
// The root is compared to the larger of its two children. If larger
// then the branch already meets the criteria for a heap. Otherwise,
// the two are swapped and the test is repeated at the next level, i.
// e. between the newly exchanged value and the children of this
// index. Stopping when the root is larger than either child works
// only if the remainder of the branch is already heaped. This is met
// initially by heapifying from the lowest parent tier backward to
// the beginning of the list.
// ..............................................................
void siftDown( int *list, int root, int last )
{
int child;
STAT( statPtr, CALLS, 1 );
for( ; ( child = lchild( root )) <= last ; root = child )
{
STAT( statPtr, COMPARES, 2 );
if( child < last && list[ child ] < list [ child + 1 ] )
++child;
if( list[ root ] < list[ child ] )
swap( list + root, list + child );
else
break;
}
}
// --------------------------------- heapify ---------------------
// Purpose: Transform the array into a heap. This is done in-place by
// swapping elements to enforce the heap criteria that every parent
// is larger than both of its children.
// Arguments: int *list is the array, int cnt is the number of
// elements in list.
// ..................... notes ....................................
// OPERATION
// This calls siftDown to heapify each branch. By starting at the
// parent of the last child and working backward to the beginning, we
// meet siftDown's requirement that lower parts of a branch be heaped
// so it can stop as soon as the element sifting down is larger than
// both of its children. Note that we are passed cnt but only use
// last, i.e. cnt - 1, first to get the last parent and then in the
// siftDown loop. Unlike the heapSort loop, last does not change
// during heapify. The root moves up to the beginning of the list but
// it is always possible that any earlier element needs to sift all
// the way to the end.
// ....................................................................
void heapify( int *list, int cnt )
{
STAT( statPtr, CALLS, 1 );
for( int root = parent( --cnt ) ; root >= 0 ; --root )
siftDown( list, root, cnt );
// Note siftDown parm 3 is last, not cnt.
}
// ------------------------ heapSort --------------------------------
// Purpose: Sort an array in-place by transforming it to a max heap
// and then removing each successive max and re-heapifying the branch
// rooted at max. This is cleverly done by swapping max with last and
// shortening the list at each iteration. This not only saves the
// elements in order without using additional memory but also ensure
// that the next larger element will move up to the max position
// using just the normal heapifying code.
// ...........................................................
void heapSort( int *list, int cnt )
{
STAT( statPtr, CALLS, 1 );
heapify( list, cnt );
for( int last = cnt - 1 ; last >= 0 ; --last )
{
swap( list, list + last );
siftDown( list, 0, last - 1 );
}
}
// ======================= QUICK SORT ==================
// Quicksort operates by choosing any element of the list to serve
// as "pivot", moving elements smaller than the pivot to its right
// and larger to its left, and recursing to sort the right and left
// sublists. Any element of a list can serve as pivot but the move
// evenly it splits the list the less recursion there will be.
// However, we can't even guess what the midpoint value is until the
// list is sorted. But, if the list is already sorted, then the
// midpoint is the best choice for pivot. This also happens to be the
// situation where quicksort performs poorly, so the worst case can
// be improved by using the midpoint.
// -------------------------------- quickSort --------------------
// .................................. notes ......................
// The procedure scans the list from left to right looking for a
// value larger than the pivot to the left of a value smaller than
// the pivot and swapping these two. The pivot value itself is
// removed from the list before this scan and is never swapped. But
// its virtual position is just after the last smaller element
// swapped. To remove the midpoint pivot without rebuilding the list,
// the value at the midpoint is replaced with the value from the
// first element. Typically, this is done by swapping, which
// conveniently saves the pivot value while plugging the hole. This
// is a good general-purpose approach, especially if swapping and
// comparison are indirect, but precludes optimization that could be
// applied if the pivot value were stored in an automatic.
// last is the index of the last swap. 0 if none else position of
// the last element smaller than pivot. After performing all gt-lt
// swaps, this element is moved into the hole at the beginning of the
// list and replaced by the pivot value.
// The swapping pivot approach is: swap list[0] with list[ cnt / 2 ]
// scan list, swapping > and < pivot elements. swap list[0] with
// list[ last ]
// The automatic pivot approach is:
// pivotVal = list[ cnt / 2 ], list[ cnt / 2 ] = list[ 0 ]
// scan list
// list[ 0 ] = list[ last ], list[ last ] = pivotVal.
// I'm using the swap because it is simpler.
// ..........................................................
void quickSort( int *list, int cnt )
{
int last;
int idx;
STAT(statPtr,CALLS,1);
STAT_DEPTH_INC;
swap( list, list + cnt / 2 );
for( last = 0, idx = 1 ; idx < cnt ; idx++ )
{
STAT(statPtr,COMPARES,1);
if( list[ idx ] < *list && idx != ++last )
swap( list + last, list + idx );
}
if( last != 0 )
swap( list, list + last ); // Pivot replaces last element < pivot.
// Recurse only on sublists that have two or more elements. last is
// the index of the pivot. If last > 1 then left contains at least 0
// and 1. If last < cnt - 2 then right contains at least cnt - 1 and
// cnt - 2.
if( last > 1 )
quickSort( list, last );
if( last < cnt - 2 )
quickSort( list + last + 1, cnt - last - 1 );
STAT_DEPTH_DEC;
}
// ---------- QUICKSORT WITH EMBEDDED SWAP ------------
// Function 'E'
// This just proves that making the swap function inline does
// actually work. However, this is slightly faster (about 0.75% than
// with inline swap function) probably due to optimization. But,
// neither makes much of a difference. quickSortEs is only 1.5%
// faster than quickSort with non-inline swap. Therefore, this sort
// is normally commented out of the function list.
// ................................................................
void quickSortEs( int *list, int cnt )
{
int last;
int idx;
int temp;
#define SWAP(I,J) temp = *(I), *(I) = *(J), *(J) = temp
STAT(statPtr,CALLS,1);
STAT_DEPTH_INC;
SWAP( list, list + cnt / 2 );
STAT( statPtr, SWAPS, 1 );
for( last = 0, idx = 1 ; idx < cnt ; idx++ )
{
STAT(statPtr,COMPARES,1);
if( list[ idx ] < *list && idx != ++last )
{
SWAP( list + last, list + idx );
STAT( statPtr, SWAPS, 1 );
}
}
if( last != 0 )
{
SWAP( list, list + last ); // Pivot replaces last element < pivot.
STAT( statPtr, SWAPS, 1 );
}
// Recurse only on sublists that have two or more elements. last is
// the index of the pivot. If last > 1 then left contains at least 0
// and 1. If last < cnt - 2 then right contains at least cnt - 1 and
// cnt - 2.
if( last > 1 )
quickSort( list, last );
if( last < cnt - 2 )
quickSort( list + last + 1, cnt - last - 1 );
STAT_DEPTH_DEC;
}
// ---------- SWAPLESS QUICKSORT -------------
// This is similar to the standard but replaces swap with simple
// copy. It does this by first making a local copy of one element,
// leaving a hole for the first copy destination, which leaves a hole
// for the second and so on. This requires toggling between searching
// from the right for an element smaller than the pivot and searching
// from the left for one larger, so that each search, if successful,
// leaves a hole for the other search. I have arbitrarily selected to
// initially copy the leftmost element so the right-to-left search
// must be first. If the first element were the pivot then copying it
// to a local used for pivot comparison would be obvious and
// potentially faster than referencing some element (as K&R do after
// swapping the midpoint pivot and leftmost element. However, we want
// to use the midpoint for pivot in case the list is already sorted
// so first the midpoint is copied to local pivot and then the
// leftmost element to the midpoint. In any case, we need a local to
// hold an element which makes indirection difficult. In the classic
// quick sort, comparison and swap are done through function pointers
// with no local element copies so the sort function doesn't need to
// know what the elements are. It would be possible to pass (directly
// or by global) the size of the element and let it cast a local
// memory block for the copy but this is unreasonably complicated.
// Instead, I'm doing only the templatized quicksort as swapless.
template <class T> void TqSort( T *list, int cnt )
{
T pivot;
int left;
int right;
STAT( statPtr, CALLS, 1 );
STAT_DEPTH_INC;
pivot = list[ cnt / 2 ];
list[ cnt / 2 ] = list[0];
left = 0;
right = cnt - 1;
while( 1 )
{
for( ; list[ right ] >= pivot ; --right )
{
STAT( statPtr, COMPARES, 1 );
if( left >= right )
goto done;
}
list[ left++ ] = list[ right ];
for( ; list[ left ] <= pivot ; ++left )
{
STAT( statPtr, COMPARES, 1 );
if( left >= right )
goto done;
}
list[ right-- ] = list[ left ];
STAT( statPtr, COMPARES, 2 );
STAT_COPIES( statPtr, 1, sizeof( int ));
}
done:
list[ left ] = pivot;
if( left > 1 )
TqSort( list, left );
if( left < cnt - 2 )
TqSort( list + left + 1, cnt - left - 1 );
STAT_DEPTH_DEC;
}
void quickSortNs( int *list, int cnt )
{
TqSort( list, cnt );
}
Even when I am sure that standard algorithms are appropriate for a particular situation, I like to know that I am applying them correctly. To give myself a theoretical base, I typically study topics in unusual depth, devising my own exercises to explore ideas. For example, automata theory teaches that an LR parser is more efficient with an RL grammar than with LR. This is logical but is still an abstraction and doesn't address the effect of imposing an RL grammar on an existing language that is more naturally LR or vice versa or whether using precedence and associativity to disambiguate flatter grammars negates any LR/RL differences. I have examined these issues theoretically and practically to design effective grammars. See my Language Design for examples. This is also how I studied Linux application IPC and communication mechanisms. See Linux App Program Examples.
Most programmers are aware that there are many sorting methods but have only a general idea of how complexity affects performance and little understanding of the practical criteria for selecting a method. Most often they either simply use the quick sort provided by a run-time library or they write their own bubble sort. My theoretical understanding of sorting was better than this but incomplete so I devised an exercise to address some issues.
We are taught, for example, that the complexity of bubble sort is On^2 and that of quick is Ologn on completely unsorted but On^2 on completely sorted lists. But this does not directly inform a practical decision. The theoretical complexity drops all but the most significant polynomial term and ignores differences in O ("big O"). These become more significant as the data set gets smaller. I wanted to know the data size thresholds of practical method complexity inflection points.
While it is true that the worst case quick is terrible, it only occurs with a presorted list, a condition that is easily avoided. But quick can consume considerable stack even in less pathologic cases. Because heap sort has the same theoretical complexity as the best case quick and there is little difference between the best and worst cases, it would seem better than quick in all situations. But the lower polynomial terms and huge big-O difference all favor quick on average. Heap may still be advised for situations with limited stack, such as sorting a kernel-level task list, but the relatively small data sets that normally appear in these situations might be better handled by a non-recursive sort with worse complexity but better big-O. Here, too, data set size method inflection points can be of significant practical value.
Many implementations of quick appear to copy the version that Kernighan and Ritchie provide in the C Programming Language. But that was intended to illustrate function pointers and is not a very good quick. It has excessive swaps and, by sorting the left and then the right subsets, requires intermediate storage, which can be avoided by sorting the two simultaneously. I wanted to make an improved version for the standard library function, which needs to retain run-time polymorphism, but I also wanted to see how much performance could be improved by a template version. This would still be polymorphic but specialization would occur at compile time.
I wrote these programs to answer these and other questions. It is not simply a theoretical exploration but also generates clear rationales for method selection in practical circumstances. I developed this under Linux but only the mechanism for controlling template instantiation is OS-specific (more precisely Linux-Gcc).
(continuation of sorts.cpp)
// ===================== TEST MANAGEMENT AND DISPLAY ========
// ------------------------ putSpace ------------------------
void putSpace( int cnt )
{
while( cnt-- > 0 )
putchar( ' ' );
}
// ----------------------------- showStats ------------------
void showStats( int *stats, int fsel = -1 )
{
if( fsel >= 0 )
putSpace( nameFieldLen - printf( "%s:", funcs[ fsel ].name ));
for( int statsel = 0 ; statsel < DIM_STATS ; ++statsel )
if( stats[ statsel ] > 0 )
printf( "%s=%d ", statNames[ statsel ], stats[ statsel ] );
putchar( '\n' );
}
// ---------------------- oneDat -------------------------
void oneDat( int fsel, int dsel )
{
int cnt;
if( dsel == DSEL_USER )
{
statPtr = stats[ fsel ][0];
cnt = userDatCnt;
memcpy( testDat, userDat, cnt * sizeof( int ));
}
else
{
statPtr = stats[ fsel ][ dsel ];
cnt = datLists[ dsel ].cnt;
memcpy( testDat, datLists[ dsel ].list, cnt * sizeof( int ));
}
memset( statPtr, 0, sizeof( stats[0][0]));
show( testDat, cnt, -1, (char*)"In: " );
depth = 0;
maxDepth = 0;
funcs[ fsel ].func( testDat, cnt );
statPtr[ DEPTH ] = maxDepth;
show( testDat, cnt, -1, (char*)"Out: " );
if( showWhat & SHOW_EACH_DAT_STAT )
showStats( statPtr );
}
// -------------- oneFunc ----------------------------------
void oneFunc( int fsel, int dsel )
{
if( showWhat & SHOW_BASIC )
printf( "***** %s ******\n", funcs[ fsel ].name );
if( dsel < DIM( datLists ) ) // -1 if user data or randList
// else index for one data list.
oneDat( fsel, dsel );
else
for( size_t dat = 0 ; dat < DIM( datLists ) ; ++dat )
{
oneDat( fsel, dat );
if( showWhat & SHOW_BASIC )
printf( "-----------\n" );
}
}
// ------------------ timeOneFunc ---------------------------
void timeOneFunc( int fsel, int dsel, int repTimes )
{
clock_t start;
clock_t ticks;
start = clock();
while( repTimes-- > 0 )
oneFunc( fsel, dsel );
ticks = clock() - start;
funcs[ fsel ].ticks = ticks; // Record for group stats
if( ticks > maxTick )
{
maxTick = ticks;
slowest = fsel;
}
printf( "%s execution time = %.2f seconds\n", funcs[ fsel ].name,
double( ticks ) / CLOCKS_PER_SEC );
}
// ----------------- randFill ----------------------------------
// Purpose: Fill array with random integers.
// If we were to just take the raw return from rand, we would get
// many large numbers, consuming unnecessary display space in use. To
// keep the numbers small, the return from rand is truncated and then
// tested against all of the numbers currently in the list. To avoid
// long run times when the list is nearly complete, at each
// uniqueness failure, the modulus is increased, allowing a larger
// range and more possibilities. Another nested loop to try several
// vals before increasing the modulus does not significantly improve
// the result.
// ..................................................................
void randFill( int *list, int cnt, bool constrain = true )
{
int idx;
int idx2;
int val;
// For extensive time testing, this program can be invoked in a shell
// loop, in which case we would want a different data set at each
// invocation. This is achieved by calling srand with a varying seed.
// For debugging, we might want the same data set each time.
if( !randomRepeat ) // Command line DR = random unique,
// DRR = random repeat.
srand( time(0));
for( idx = 0 ; idx < cnt ; idx++ )
{
if( !constrain )
list[ idx ] = rand();
else
{
for( int limit = cnt ; ; limit += cnt / 8 )
{
val = rand() % limit;
for( idx2 = 0 ; idx2 < idx ; ++idx2 )
if( val == list[ idx2 ] )
break; // This val is a repeat
if( idx2 == idx )
{
list[ idx ] = val;
break; // Break the limit loop.
}
}
}
}
}
// --------------------- printWid ----------------------------
int printWid( int width, char *str )
{
int len;
char* cp2;
char* cp;
int cnt = 0;
cp = str;
while( 1 )
{
len = strlen( cp );
if( len >= width )
{
for( cp2 = cp + len - 1 ;
len >= width || !isspace( *cp2 ) ; --cp2, --len )
;
}
else
cp2 = 0;
cnt += printf( "%*.*s", len, len, cp );
if( cp2 != 0 )
{
printf( "\n " );
cp = cp2;
}
else
return cnt;
}
}
// ----------------------------- usage ---------------------------
void usage( void )
{
// The environment contains LINE and COLUMNS variables but they are
// completely wrong. To get the correct values use tput LINES and
// tput COLS. LINES and COLS are termcap names. Supposedly, these
// come from the terminfo database but the values change when the
// window is resized. Also, supposedly, tput is based on ncurses, but
// curses documentation says nothing about reading caps. The only
// means may be to spawn tput and somehow read its output, perhaps
// with a pipe.
int width = 80;
printWid( width,
(char*)"sorts demonstrates and tests various sorting functions.\n" );
printWid( width,
(char*)"With no arguments, apply each sort function to five built in \
data sets, displaying each data set before and after sorting and total\
statistics.\n" );
printWid( width,
(char*)"Fx invokes one or more functions selected by x. F-x \
invokes all but the functions selected by x. x is any \
combination of (!=default excluded):\n" );
for( int idx = 0 ; idx < DIM( funcs ) ; idx++ )
printf( "%d/%c=%s%c ", idx, funcs[ idx ].cid,
funcs[ idx ].name, funcs[ idx ].select ? ' ' : '!' );
putchar( '\n' );
printWid( width,
(char*)"Dx selects only one of the five (0-4) data sets.\n" );
printWid( width,
(char*)"DRx selects a single data set of x random integers, \
which is different at each invocation. DRRx produces the same \
set at each invocation.\n" );
printWid( width,
(char*)"Tx requests that the sort(s) be invoked x times. The \
execution time is reported. In this mode no other information \
is displayed.\n" );
printWid( width,
(char*)"A space-delimited list of numbers is taken as the one \
and only data set to be sorted.\n" );
printWid( width,
(char*)"Rx produces a list of x random integers to be used in \
a subsequent invocation or pasted into the code. The range is \
loosely bounded by x.\n" );
}
// ------------------- main ----------------------------------
int main( int argc, char **argv )
{
int total[ DIM_STATS ];
int statsel;
int cnt;
int idx;
char* cp;
int dsel = DSEL_ALL;
int repTimes = 0;
int nFuncs = DIM( funcs );
bool userDatRand = false;
showWhat = SHOW_BASIC;
userDatCnt = 0;
userDat = 0;
for( int arg = 1 ; arg < argc ; arg++ )
{
switch( toupper( *argv[ arg ]) )
{
case '-':
case 'H':
usage();
return 0;
case 'F': // Function selector
bool addFuncs;
// By default, all functions are selected but if the command line
// includes F then deselect all except the ones selected by F, e.g.
// F01234 or Fbsmhq
if( argv[ arg ][1] == '-' )
{
cnt = 2; // function list starts after '-'
addFuncs = false;
nFuncs = DIM( funcs );
}
else
{
cnt = 1; // function list starts after 'F'
addFuncs = true;
nFuncs = 0;
for( idx = 0 ; idx < DIM( funcs ) ; idx++ )
funcs[ idx ].select = false;
}
for( ; argv[ arg ][ cnt ] != 0 ; cnt++ )
{
if( isdigit( argv[ arg ][cnt]) )
{
idx = argv[ arg ][ cnt ] - '0';
if( idx >= DIM( funcs ) )
{
printf( "Illegal function selector %d. \
Range is 0-%d\n", idx, DIM( funcs )- 1 );
return 1;
}
}
else
{
for( idx = 0 ; ; ++idx )
{
if( idx == DIM( funcs ) )
{
printf( "Unrecognized function %s\n",
argv[ arg ] + cnt );
return 1;
}
if( funcs[ idx ].cid == toupper( argv[ arg ][ cnt ] ) )
break;
}
}
if( addFuncs )
{
nFuncs++;
funcs[ idx ].select = true;
}
else
{
nFuncs--;
funcs[ idx ].select = false;
}
}
break; // case 'F'
case 'D': // Data set selector.
cp = argv[ arg ] + 1;
if( toupper( *cp++ ) == 'R' )
{
if( toupper( *cp ) == 'R' ) // "Repeatable"
{
randomRepeat = true;
cp++;
}
userDatCnt = atoi( cp );
userDat = (int *)malloc( userDatCnt * sizeof( int ));
userDatRand = true; // For delayed fill after collecting
// all args in case of T.
}
else
{
dsel = atoi( argv[ arg ] + 1 );
if( dsel < 0 || dsel >= DIM( datLists ) )
{
printf( "Bad data set selector %d. Only 0-%d supported.\n",
dsel, DIM( datLists ) - 1 );
return 1;
}
}
break;
case 'T': // Time. Display execution time of multiple invocations.
repTimes = atoi( argv[ arg ] + 1 );
break;
case 'R': // Generate small unique random numbers for pasting
// into this program or command line.
cnt = atoi( argv[ arg ] + 1 );
userDat = (int *)malloc( cnt * sizeof( int ));
randFill( userDat, cnt );
for( idx = 0 ; idx < cnt ; ++idx )
{
printf( "%d", userDat[ idx ]);
putchar( idx == cnt - 1 ? '\n' : ',' );
}
free( userDat );
return 0;
default:
if( isdigit( *argv[ arg ]) )
{
if( userDat == 0 )
userDat = (int *)malloc( MAX_USER_INPUT_DAT * sizeof( int ));
if( userDatCnt >= MAX_USER_INPUT_DAT )
{
printf( "Too much data. Limit is %d\n", MAX_USER_INPUT_DAT );
free( userDat );
return 1;
}
userDat[ userDatCnt++ ] = atoi( argv[ arg ]);
}
else
{
printf( "Unrecognized option %d\n", *argv[ arg ]);
return 1;
}
}
}
if( userDatCnt > 0 )
{
dsel = DSEL_USER;
cnt = userDatCnt;
// We delayed filling DRx data list until collecting all command line
// arguments in case T occurs after DRx because, when timing, the
// data values are not displayed so we don't care how large they are
// or even whether they are unique. For timing a few duplicates
// wouldn't matter. But the randFill constrained is very slow, e.g 15
// seconds to fill 100K list. Coincidentally, large lists are of most
// interest when timing, which is when we are least likely to be
// interested in the actual data. If repTimes is 0 then we are not
// timing and the constrain argument to randFill is true.
if( userDatRand )
randFill( userDat, userDatCnt, repTimes == 0 );
}
else
cnt = 100;
testDat = (int *)malloc( cnt * sizeof( int ));
if( repTimes != 0 )
{
showWhat = SHOW_NOTHING; // Printing reduces timing accuracy.
printf( "Starting\n" ); // Depending on how the random
// list is created, there may be a long delay before sorting begins
// so it's good to indicate this.
maxTick = 0;
for( idx = 0 ; idx < DIM( funcs ) ; idx++ )
if( funcs[ idx ].select )
timeOneFunc( idx, dsel, repTimes ); // Apply one
// function to one or more lists.
for( idx = 0 ; idx < DIM( funcs ) ; idx++ )
if( funcs[ idx ].select )
printf( "%s time = %ld%%\n", funcs[ idx ].name,
maxTick == 0 ? 0L :
long(( funcs[ idx ].ticks * 100 ) / maxTick ));
} // repTimes != 0
else if( nFuncs == 1 ) // repTimes == 0 && nFuncs == 1
{
showWhat |= SHOW_EACH_DAT_STAT;
// Search for the one selected function. While processing F argument
// we could have easily recorded the one function selected by Fx but
// not the one function remaining after F-x so, instead, we just
// search for it here.
for( idx = 0 ; idx < DIM( funcs ) ; idx++ )
if( funcs[ idx ].select )
{
oneFunc( idx, dsel );
break;
}
}
else // repTimes == 0 && nFuncs != 1
{
for( idx = 0 ; idx < DIM( funcs ) ; idx++ )
if( funcs[ idx ].select )
oneFunc( idx, dsel ); // Apply one function to
// one or more lists.
if( dsel >= DIM( datLists ) )
{
// For each data set show the stats of each function.
for( dsel = 0 ; dsel < (int)DIM( datLists ) ; ++dsel )
{
show( datLists[ dsel ].list, datLists[ dsel ].cnt, -1 );
for( idx = 0 ; idx < DIM( funcs ) ; ++idx )
if( funcs[ idx ].select )
showStats( stats[ idx ][ dsel ], idx );
}
}
} // nFuncs != 1
// Show the total stats of each function across all data sets.
printf( "Totals:\n" );
for( idx = 0 ; idx < DIM( funcs ) ; ++idx )
{
if( funcs[ idx ].select )
{
memset( total, 0, sizeof( total ));
for( statsel = 0 ; statsel < DIM_STATS ; ++statsel )
{
for( dsel = 0 ; dsel < (int)DIM( datLists ) ; ++dsel )
total[ statsel ] += stats[ idx ][ dsel ][ statsel ];
}
showStats( total, idx );
}
}
free( testDat );
if( userDat != 0 )
free( userDat );
return 0;
}
/*********************** txqsort.cpp ***************************
Description: GNU C++ program to demonstrate templatized quick sort
with explicit instantiation of an int and a double version in another
module. This demonstrates the extern solution to controlling
instantiation, which is the approach that most compilers (most
importantly GNU) are converging on.
...................... notes ................................
EXTERN TEMPLATE
The extern approach to controlling template instantiation requires,
as do most solutions, the template source to reside in the header.
Thus, it cannot be hidden and the compiler must at least scan it.
Crude (e.g. Microsoft) solutions generate code at every invocation of
the template and the linker subsequently removes all but one
instance. With extern, the code is not instantiated at any invocation
but only at a fully-qualified declaration. In this demonstation,
there are two of these in the txqs.cpp:
template void TqSort( int*, int );
template void TqSort( double*, int );
These match the extern declarations in txqsort.h:
extern template void TqSort( int *list, int cnt );
extern template void TqSort( double *list, int cnt );
Besides being unable to hide the code and forcing the compiler to
process it repeated, this approach forces the programmer to declare
up front which forms of the template will be used. However, it isn't
necessary to make all forms explicit. Ones that are used a lot could
be explicit to reduce build time. Any forms not made explicit will
still work but just increase the build time if they have more than
one instance.
MAKE
This requires two modules, qtest.cpp and qst.cpp. qst.cpp contains
only the template explicit declarations. It is used to show how a
chosen module can be the instantiator.
txqsort: txqsort.o txqs.o
g++ -o $@ $?
rm *.o
%.o: %.cpp
g++ -ggdb3 -std=c++0x -Wall -c $<
****************************************************************/
#include <stdio.h>
#include "txqsort.h"
#define DIM(A) (int)(sizeof(A)/sizeof(A[0]))
int dat[] = { 3, 2, 5, 8, 6, 0, 1};
double dat2[] = { 3.6, 3.5, 2.0, 4.5, 6.0, 5.5};
int main( int argc, char **argv )
{
int idx;
TqSort( dat, DIM( dat ));
for( idx = 0 ; idx < DIM( dat ) ; idx++ )
printf( "%d, ", dat[ idx ]);
putchar( '\n' );
TqSort( dat2, DIM( dat2 ));
for( idx = 0 ; idx < DIM( dat2 ) ; idx++ )
printf( "%f, ", dat2[ idx ]);
putchar( '\n' );
return 0;
}
/************************** txqsort.h ********************************
Description: txqsort program demonstrates control of template
instantiation by extern specialization declarations in the header.
See txqsort.cpp and txqs.cpp.
************************************************************/
template <class T> inline void Tswap( T& one, T& two )
{
T temp;
temp = two;
two = one;
one = temp;
}
template <class T> void TqSort( T *list, int cnt )
{
int last;
int idx;
Tswap( list[0], list[ cnt / 2 ]);
for( last = 0, idx = 1 ; idx < cnt ; ++idx )
if( list[ idx ] < list[0] && ++last != idx )
Tswap( list[ idx ], list[ last ]);
Tswap( list[0], list[ last ]);
if( last > 1 )
TqSort( list, last );
if( last < cnt - 2 )
TqSort( list + last + 1, cnt - last - 1 );
}
extern template void TqSort( int *list, int cnt );
extern template void TqSort( double *list, int cnt );
/*********************** txqsort.cpp ***************************
Description: GNU C++ program to demonstrate templatized quick sort
with explicit instantiation of an int and a double version in another
module. This demonstrates the extern solution to controlling
instantiation, which is the approach that most compilers (most
importantly GNU) are converging on.
...................... notes ................................
EXTERN TEMPLATE
The extern approach to controlling template instantiation requires,
as do most solutions, the template source to reside in the header.
Thus, it cannot be hidden and the compiler must at least scan it.
Crude (e.g. Microsoft) solutions generate code at every invocation of
the template and the linker subsequently removes all but one
instance. With extern, the code is not instantiated at any invocation
but only at a fully-qualified declaration. In this demonstation,
there are two of these in the txqs.cpp:
template void TqSort( int*, int );
template void TqSort( double*, int );
These match the extern declarations in txqsort.h:
extern template void TqSort( int *list, int cnt );
extern template void TqSort( double *list, int cnt );
Besides being unable to hide the code and forcing the compiler to
process it repeated, this approach forces the programmer to declare
up front which forms of the template will be used. However, it isn't
necessary to make all forms explicit. Ones that are used a lot could
be explicit to reduce build time. Any forms not made explicit will
still work but just increase the build time if they have more than
one instance.
MAKE
This requires two modules, qtest.cpp and qst.cpp. qst.cpp contains
only the template explicit declarations. It is used to show how a
chosen module can be the instantiator.
txqsort: txqsort.o txqs.o
g++ -o $@ $?
rm *.o
%.o: %.cpp
g++ -ggdb3 -std=c++0x -Wall -c $<
****************************************************************/
#include <stdio.h>
#include "txqsort.h"
#define DIM(A) (int)(sizeof(A)/sizeof(A[0]))
int dat[] = { 3, 2, 5, 8, 6, 0, 1};
double dat2[] = { 3.6, 3.5, 2.0, 4.5, 6.0, 5.5};
int main( int argc, char **argv )
{
int idx;
TqSort( dat, DIM( dat ));
for( idx = 0 ; idx < DIM( dat ) ; idx++ )
printf( "%d, ", dat[ idx ]);
putchar( '\n' );
TqSort( dat2, DIM( dat2 ));
for( idx = 0 ; idx < DIM( dat2 ) ; idx++ )
printf( "%f, ", dat2[ idx ]);
putchar( '\n' );
return 0;
}
/****************** txqs.cpp ***************************************** Description: txqsort program demonstrates control of template instantiation by extern specialization declarations in the header. This module instantiates the int and and double specializations of TqSort (quicksort) defined in txqsort.h and actually used in txqsort. cpp. ********************************************************************/ #include <stdio.h> #include "txqsort.h" template void TqSort( int*, int ); template void TqSort( double*, int );